
Le questionnaire de Proust : Roberto Natalini
 Roberto Natalini est directeur de recherche au CNR (le conseil national de recherche en Italie), affecté à l'Istituto per le Applicazioni del Calcolo "Mauro Picone" de Rome. Ses intérêts de recherche concernent principalement l'analyse mathématique et numérique des équations aux dérivées partielles (en particulier de type hyperbolique et parabolique) appliquées à la biologie, à la conservation des monuments, au trafic routier et à la dynamique des gaz.
Roberto Natalini est directeur de recherche au CNR (le conseil national de recherche en Italie), affecté à l'Istituto per le Applicazioni del Calcolo "Mauro Picone" de Rome. Ses intérêts de recherche concernent principalement l'analyse mathématique et numérique des équations aux dérivées partielles (en particulier de type hyperbolique et parabolique) appliquées à la biologie, à la conservation des monuments, au trafic routier et à la dynamique des gaz.
Il est membre du conseil directif de la SIMAI (la société italienne de mathématiques appliquées et industrielles) et coordinateur du site MaddMaths! italien (http://maddmaths.simai.eu/). Depuis juillet 2012 il est responsable scientifique du Guichet des Mathématiques pour l'Industrie Italienne (http://sportellomatematico.it/).
- Ma vertu préférée en mathématiques
Le courage (ou bien l'imagination, je n'arrive pas bien à choisir)
- Le principal trait de mon caractère mathématique
L'inconscience
- La qualité que je préfère chez les mathématiciens
La clarté
- La qualité que je préfère en mathématiques
La capacité de connecter des idées lointaines
- Mon principal défaut comme mathématicien
Être brouillon
- Ma lecture mathématique préférée
Les livres de pensées de Giancarlo Rota (mais j'ai aussi bien aimé «What is Mathematics, really?» par Reuben Hersh).
- Mon rêve comme mathématicien / Mon cauchemar comme mathématicien.
Avoir une idée simple, mais profonde / La même idée le lendemain matin
- La faiblesse principale des mathématiques
L'arrogance
- Le mathématicien que je voudrais être
Euler (mais il me suffirait d'être Vito Volterra)
- Le pays où je voudrais vivre.
Cela pourrait paraître bizarre, mais j'aime bien vivre en Italie. Ou bien le sud
de la France (mais pas de pays froids, s'il vous plaît).
- L'exercice de mathématiques que je préfère
Les calculs des solutions exactes des équations aux dérivées partielles (quand il y en a).
- Le théorème que je préfère
Le théorème de Lax de l'existence des solutions du problème de Riemann pour les lois de conservation hyperboliques.
- L'application des mathématiques que je préfère
Pour un exposé grand public : l'algorithme PageRank de Google. Pour moi : la biologie cellulaire (j'ai des travaux en cours pour arriver à un modèle satisfaisant de cellule eucaryote).
- Les mathématiciens qui m'ont orienté
Maria Giovanna Garroni, Bernard Hanouzet
- Les mathématiciens qui m'ont dissuadé
Je ne sais/veux pas répondre (et je suis bien parmi ceux qui ont conçu ce questionnaire...)
- Le nom de variable que je préfère
Eta (ici il y aurait au moins trois jeux de mots à faire, mais le premier marche seulement en italien, et on ne comprendra jamais le deuxième en France...).
- Le type de calcul que je préfère
Facile.
- Le type de calcul que j'utilise
Estimations de l'énergie.
- Le type de calcul que je trouve le plus ennuyeux
Calcul des conditions au bord numériques pour les problèmes paraboliques avec des conditions de type Neumann. J'oublie toujours les signes des coefficients.
- Les dénominations mathématiques que je préfère (théorème, corollaire...)
Définition.
- L'entreprise scientifique que j'estime le plus
L'invention de l'ordinateur.
- Le don de la nature que je voudrais avoir.
Plus d'imagination.
- Comment j'aimerais qu'on se souvienne de moi comme mathématicien
Un type enthousiaste et avec lequel il était intéressant de parler.
- L'état présent de mes recherches
J'avance doucement.
- La faute qui m'inspire le plus d'indulgence
Les fautes de signe.
- Ma devise
Te occidere possunt sed te edere non possunt nefas est (Ils peuvent te tuer, mais ils ne peuvent pas te manger, c'est illégal).
- Pourquoi la recherche mathématique est-elle masculine ?
Personnellement j'aurais même tendance à penser le contraire. J'ai plus de collaborations avec des femmes qu'avec des hommes. En ce sens, les maths sont pour moi assez féminines ! Mais je sais que ce n'est pas le cas général. Les maths demandent beaucoup de temps (et d'inconscience). Les femmes, souvent, sont dépossédées du temps qu'elles pourraient avoir à cause du modèle familial traditionnel. Quoi qu'il en soit, c'est un sujet important et délicat qui mériterait qu'on y consacre plus que quelques lignes.
- Les mathématiques appliquées s'étendent-elles à la même vitesse que celle des algorithmes mathématiques ?
Je dirais même davantage.
- Dans quelle mesure le travail compte-t-il dans la résolution de problèmes mathématiques ?
Beaucoup, presqu'à 90 %, même quand on a beaucoup de talent.
- Dans quelle mesure le formalisme compte-t-il ?
C'est essentiel.
- Mathématiques et grammaire sont-elles liées ?
Les mathématiques sont plutôt liées au langage. La grammaire est un outil secondaire.
- Parlez-vous "mathématique" correctement ?
Pas trop. Je confonds toujours le numérateur et le dénominateur.
- À quel point faut-il être doué pour réussir en mathématique ? Pour quoi faut-il avoir moins de trente ans ?
Disons que le fait d'être doué aide beaucoup. Mais ce n'est pas tout. Il faut avoir moins de trente ans pour commencer une théorie révolutionnaire, mais pas pour la finir.
- Êtes-vous doué ? Depuis quand ?
Pas trop.

Alphabet : D comme distance
Beaucoup de concepts mathématiques ne sont en réalité que le résultat de la formalisation, ou la clarification d'« objets » concrets ; par exemple, la notion de « distance ».
 « Quelle est la distance de chez moi au travail », « combien de temps faut-il pour se rendre à tel endroit », ... sont toutes des pensées qui communément, spontanément, viennent dans nos esprits.
« Quelle est la distance de chez moi au travail », « combien de temps faut-il pour se rendre à tel endroit », ... sont toutes des pensées qui communément, spontanément, viennent dans nos esprits.
Il y a plusieurs « types » de distances. Une distance à vol d'oiseau, par exemple, est différente de celle qu'on trouve en parcourant une route. En plus des distances physiques, il y a les distances temporelles et même là, la situation peut être de nature différente : combien de temps cela va-t-il prendre ? Vais-je y aller à pied, en voiture, en vélo, en bus ?
Chaque distance est relative à un problème, à une situation différente. C'est une caractéristique des mathématiques : découvrir que certaines quantités, que l'on introduit dans des contextes différents, en réalité sont des exemples d'un même concept abstrait. C'est de là qu'on déduit une définition, c'est-à-dire qu'on arrive à définir précisément le sens d'un certain mot.
On baptise alors « distance » un objet qui possède certaines propriétés, afin de rendre clair et non ambigu pour tous ce concept. Il s'agit de déterminer un vocabulaire commun pour tous les mathématiciens.
une propriété de minimisation
La propriété la plus importante de la distance est une propriété de « minimisation ». L'idée est que la distance est toujours celle qui correspond à la valeur minimale par rapport à de nombreuses stratégies possibles. Si, par exemple, on demande la distance entre Paris et Lyon, on se réfère à la route minimale qu'il faut parcourir ; on ne va pas chercher à passer par Bordeaux ou Rennes, on cherche l'itinéraire le plus direct. La formalisation de cette propriété de minimisation est donnée par la fameuse inégalité triangulaire : la distance de Paris à Lyon est plus petite que (ou au plus égale à) celle de Paris à une troisième localité, plus celle de cet endroit à Lyon. Passer vers un troisième endroit ne peut pas raccourcir le chemin (au mieux la longueur est la même).
En général, on considère deux autres propriétés pour une distance. L'une de ces propriétés est que des points différents se trouvent toujours à une distance strictement positive (en d'autres termes, on interdit le don d'ubiquité ou la possibilité de téléportation). L'autre est celle de symétrie : pour aller de Paris à Lyon on doit faire les mêmes kilomètres que pour aller de Lyon à Paris. Mais il y a des cas, dans la vie réelle, où la symétrie n'est pas vérifiée. Prenons le cas des rues à sens unique : parfois aller d'un endroit à un autre en voiture peut être beaucoup plus court que le voyage de retour...
Quel est l'avantage d'introduire le nom de distance ?
Enfin, on se demande : quel est l'avantage d'introduire le nom de distance ? Essentiellement, c'est de voir sous un même point de vue des problèmes différents. Objets et quantités introduits dans un cas peuvent en effet être transportés à l'autre et cela peut être extrêmement rentable. Donc on espère (et cela arrive souvent) résoudre deux problèmes pour le prix d'un. Simple question de commodité...
Traduit à partir de la version originale en italien de Corrado Mascia avec l'autorisation de l'auteur.

L'analyse mathématique aide à démêler les chromosomes des bactéries
 Quand une cellule de l'Escherichia coli se divise, elle doit dupliquer son chromosome circulaire et pousser les anneaux créés pour qu'ils aillent se fixer dans deux nouvelles cellules. Cette procédure, semblable au tour de magie où l'on sépare deux anneaux métalliques, peut paraître simple, mais en réalité dénouer et séparer les ADN enlacés est bien plus complexe.
Quand une cellule de l'Escherichia coli se divise, elle doit dupliquer son chromosome circulaire et pousser les anneaux créés pour qu'ils aillent se fixer dans deux nouvelles cellules. Cette procédure, semblable au tour de magie où l'on sépare deux anneaux métalliques, peut paraître simple, mais en réalité dénouer et séparer les ADN enlacés est bien plus complexe.
Dans une étude récente, publiée en ligne dans le journal « Proceedings of the National Academy of Sciences », la professeure de mathématiques Mariel Vazquez (San Francisco) et une équipe internationale de scientifiques proposent une étude mathématique analysant comment ces chromosomes sont déconnectés par l'enzyme de recombinaison XerCD.
Certains antibiotiques, comme la ciprofloxacine, prescrits pour les infections de Escherichia coli, ciblent les enzymes responsables de la déconnection de l'ADN. Mais les cellules bactériennes traitées par ces médicaments peuvent trouver d'autre moyens de se séparer, comme celles présentées dans l'étude de M. Vazquez, leur permettant de survivre (rendant donc inutile l'action de l'antibiotique). La compréhension du processus de déconnection « peut aussi conduire à la fabrication de meilleurs médicaments anti-bactériens, avec un effet clairement positif sur la santé humaine », observe M. Vazquez.
Comprendre les infections bactériennes
Les infections par l'Escherichia coli et d'autres bactéries représentent un risque élevé pour la santé humaine. Selon le centre américain de contrôle des maladies et de la prévention, chaque année au moins deux millions de personnes sont infectées par des bactéries résistant aux antibiotiques et au moins vingt-trois mille personnes meurent chaque année suite à ces infections. Et pour comprendre les infections bactériennes, il est essentiel d'étudier comment les cellules comme l'Escherichia coli se dupliquent.
Des expériences biologiques ont donné à M. Vazquez et à ses collègues des indices concernant la séparation de chromosomes de l'Escherichia coli avant la séparation cellulaire. Cependant, ces expériences ne fournissent pas un cadre clair à toutes les étapes qui composent la séparation cellulaire.
Pour compléter ce cadre, les chercheurs proposent une analyse mathématique rigoureuse qui utilise une méthode d'enchevêtrement pour décrire les changements qui ont lieu pendant la séparation, étape par étape. Dans ce cas, « l'enchevêtrement » représente deux sites spécifiques du chromosome, liés par une enzyme de recombinaison. Les chromosomes liés après la duplication sont convertis en nœuds, puis en liens, puis en nœuds, jusqu'à ce qu'il reste deux cercles.
Les chercheurs considèrent que d'autres expériences biologiques aideraient à justifier ce modèle mathématique, mais avouent que ces expériences seraient extrêmement difficiles à produire. « Même sans ces expériences, l'analyse mathématique est une avancée significative par rapport aux études biologiques précédentes », a dit M. Vazquez.
De plus, M. Vazquez souligne que les mathématiques, la physique, l'informatique et les statistiques jouent un rôle important en biologie pour la compréhension de la topologie de l'ADN.
l'ADN n'est pas qu'une séquence de lettres
Selon M. Vazquez « il est important que les gens sachent que l'ADN n'est pas qu'une séquence de lettres. C'est une très longue molécule qui peut prendre des structures tri-dimensionnelles complexes quand il est situé dans un noyau cellulaire. Tout processus biologique qui concerne l'ADN sera affecté par cette topologie, et les changements topologiques peuvent avoir des implications biologiques importantes ».

Calcul mental avec l'aide... du chocolat chaud !
 Le chocolat pourrait nous aider à mieux aborder les mathématiques ? Selon une étude menée à l'Université de Northumbria (Royaume-Uni) il semblerait que oui : en effet pour les individus qui avaient pris de grandes quantités de flavanols (composés présents dans une tasse de chocolat chaud), le calcul mental devenait beaucoup plus abordable.
En outre, ces volontaires courageux se sentaient plus résistants et ressentaient moins la fatigue.
Le chocolat, concluent les chercheurs, pourrait être utile pour des activités qui stimulent l'esprit. Les flavanols, auteurs de ces « miracles », appartiennent à la famille des polyphénols qui augmentent le débit sanguin dans le cerveau.
Le chocolat pourrait nous aider à mieux aborder les mathématiques ? Selon une étude menée à l'Université de Northumbria (Royaume-Uni) il semblerait que oui : en effet pour les individus qui avaient pris de grandes quantités de flavanols (composés présents dans une tasse de chocolat chaud), le calcul mental devenait beaucoup plus abordable.
En outre, ces volontaires courageux se sentaient plus résistants et ressentaient moins la fatigue.
Le chocolat, concluent les chercheurs, pourrait être utile pour des activités qui stimulent l'esprit. Les flavanols, auteurs de ces « miracles », appartiennent à la famille des polyphénols qui augmentent le débit sanguin dans le cerveau.
Dans l'étude, il a été demandé à trente individus de compter en arrière avec un pas de trois, à partir d'un nombre aléatoire généré par un ordinateur entre 800 et 999. Les résultats ont montré que ceux qui avaient consommé la boisson chaude pourrait faire des calculs plus rapidement et avec plus de précision.
Un résultat qui, cependant, ne se reproduisait pas lorsque le pas a été porté à sept, une action plus complexe qui, selon les chercheurs, sollicitait une autre partie du cerveau.
Peut-être exigeait-elle un peu de crème chantilly !

Opération passage
 Imaginez une énigme, un casse-tête, ou un problème issu d'une situation concrète. Vous réfléchissez en cours, avec votre professeur et les autres élèves, à des manières de résoudre ce problème. Les maths arrivent par la petite porte... par la meilleure porte !
Imaginez une énigme, un casse-tête, ou un problème issu d'une situation concrète. Vous réfléchissez en cours, avec votre professeur et les autres élèves, à des manières de résoudre ce problème. Les maths arrivent par la petite porte... par la meilleure porte !
C'est naturellement que les notions sont précisées ; un résultat est même compris avant qu'il soit exprimé... Oui, les maths par la discussion, par l'intuition, par la recherche (de solution), par la présence d'un chercheur en mathématiques à votre cours qui prend du temps pour vous exprimer ce qui l'enthousiasme dans les maths, c'est l'opération Passage. Elle est à destination des élèves de primaire, collège et lycée, dans un cadre de formation continue mutuelle pour leur enseignant. L'enseignant et un chercheur "passeur" "partagent" la classe et préparent ensemble les passages réguliers du chercheur/passeur dans la classe. L'opération est proposée par l'institut de recherche en enseignement des mathématiques (IREM) d'Orléans depuis la rentrée de septembre 2013.
Cette action est soutenue par l'Académie d'Orléans-Tours, Animaths, Apmep, Cap Maths, Centre Galois, Centre Sciences FDP, MAPMO. Pour en savoir plus vous pouvez consulter le site internet: http://www.univ-orleans.fr/ires/irem/operation-passage.






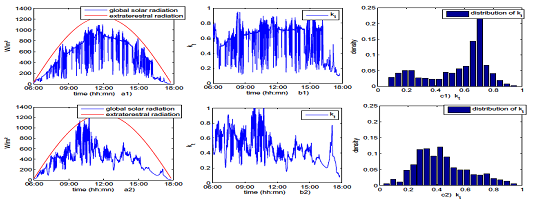
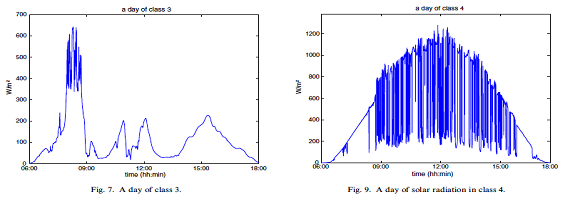
 La part de ces énergies dans le parc énergétique reste cependant en deçà des objectifs annoncés pour plusieurs raisons : choix politiques, rentabilité, difficultés technologiques, mais surtout caractère hautement aléatoire et intermittent des ressources, que nous illustrons dans la section suivante.
La part de ces énergies dans le parc énergétique reste cependant en deçà des objectifs annoncés pour plusieurs raisons : choix politiques, rentabilité, difficultés technologiques, mais surtout caractère hautement aléatoire et intermittent des ressources, que nous illustrons dans la section suivante.
 Que font les mathématiciens ? Elodie Hérault a répondu à nos questions. Elle est ingénieure en traitement d'image chez Metso-Cisa (industrie minière et construction)
Que font les mathématiciens ? Elodie Hérault a répondu à nos questions. Elle est ingénieure en traitement d'image chez Metso-Cisa (industrie minière et construction)








 Roberto Natalini est directeur de recherche au CNR (le conseil national de recherche en Italie), affecté à l'Istituto per le Applicazioni del Calcolo "Mauro Picone" de Rome. Ses intérêts de recherche concernent principalement l'analyse mathématique et numérique des équations aux dérivées partielles (en particulier de type hyperbolique et parabolique) appliquées à la biologie, à la conservation des monuments, au trafic routier et à la dynamique des gaz.
Roberto Natalini est directeur de recherche au CNR (le conseil national de recherche en Italie), affecté à l'Istituto per le Applicazioni del Calcolo "Mauro Picone" de Rome. Ses intérêts de recherche concernent principalement l'analyse mathématique et numérique des équations aux dérivées partielles (en particulier de type hyperbolique et parabolique) appliquées à la biologie, à la conservation des monuments, au trafic routier et à la dynamique des gaz. « Quelle est la distance de chez moi au travail », « combien de temps faut-il pour se rendre à tel endroit », ... sont toutes des pensées qui communément, spontanément, viennent dans nos esprits.
« Quelle est la distance de chez moi au travail », « combien de temps faut-il pour se rendre à tel endroit », ... sont toutes des pensées qui communément, spontanément, viennent dans nos esprits.
 Quand une cellule de l'Escherichia coli se divise, elle doit dupliquer son chromosome circulaire et pousser les anneaux créés pour qu'ils aillent se fixer dans deux nouvelles cellules. Cette procédure, semblable au tour de magie où l'on sépare deux anneaux métalliques, peut paraître simple, mais en réalité dénouer et séparer les ADN enlacés est bien plus complexe.
Quand une cellule de l'Escherichia coli se divise, elle doit dupliquer son chromosome circulaire et pousser les anneaux créés pour qu'ils aillent se fixer dans deux nouvelles cellules. Cette procédure, semblable au tour de magie où l'on sépare deux anneaux métalliques, peut paraître simple, mais en réalité dénouer et séparer les ADN enlacés est bien plus complexe.
 Le chocolat pourrait nous aider à mieux aborder les mathématiques ? Selon une étude menée à l'Université de Northumbria (Royaume-Uni) il semblerait que oui : en effet pour les individus qui avaient pris de grandes quantités de flavanols (composés présents dans une tasse de chocolat chaud), le calcul mental devenait beaucoup plus abordable.
En outre, ces volontaires courageux se sentaient plus résistants et ressentaient moins la fatigue.
Le chocolat, concluent les chercheurs, pourrait être utile pour des activités qui stimulent l'esprit. Les flavanols, auteurs de ces « miracles », appartiennent à la famille des polyphénols qui augmentent le débit sanguin dans le cerveau.
Le chocolat pourrait nous aider à mieux aborder les mathématiques ? Selon une étude menée à l'Université de Northumbria (Royaume-Uni) il semblerait que oui : en effet pour les individus qui avaient pris de grandes quantités de flavanols (composés présents dans une tasse de chocolat chaud), le calcul mental devenait beaucoup plus abordable.
En outre, ces volontaires courageux se sentaient plus résistants et ressentaient moins la fatigue.
Le chocolat, concluent les chercheurs, pourrait être utile pour des activités qui stimulent l'esprit. Les flavanols, auteurs de ces « miracles », appartiennent à la famille des polyphénols qui augmentent le débit sanguin dans le cerveau.
 Imaginez une énigme, un casse-tête, ou un problème issu d'une situation concrète. Vous réfléchissez en cours, avec votre professeur et les autres élèves, à des manières de résoudre ce problème. Les maths arrivent par la petite porte... par la meilleure porte !
Imaginez une énigme, un casse-tête, ou un problème issu d'une situation concrète. Vous réfléchissez en cours, avec votre professeur et les autres élèves, à des manières de résoudre ce problème. Les maths arrivent par la petite porte... par la meilleure porte !