Talk

Growth fragmentation models in oncology.
Florence Hubert (Aix-Marseille Université)

Growth fragmentations models are often used in structured population dynamics to model for example cell division, polymerization. The classical form of the equation is The wellposeness of a solution globally defined to this equation as well as its asympototic behaviour has been widely studied. We will first give some contexts where this model is used. We will then recall the main results (see [1], [4]). We will also propose extensions of such equation in the context of metastasis spreading and in the context of microtubule dynamical instabilities. We will make a point on the properties of these models and the remaining challenges.

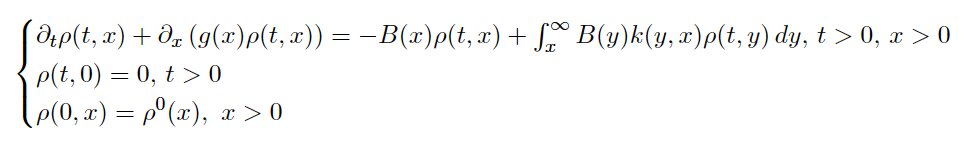
References
[1] J. A. Cañizo, P. Gabriel, and H. Yoldas. Spectral gap for the growthfragmentation equation via Harris’s theorem. SIAM J. Math. Anal., Vol.53, No.5, pp.5185-5214,(2021)
[2] N. Hartung, S. Mollard, D. Barbolosi, A. Benabdallah, G. Chapuisat, G. Henry,S. Giacometti, A. Iliadis, J.Ciccolini, C. Faivre, F. Hubert. Mathematical Modeling of tumor growth and metastatics spreading : validation in tumor-bearing mice, Cancer Research 74, p. 6397-6407, 2014.
[3] S. Honoré, F. Hubert, M. Tournus, D. White. A growth-fragmentation approach for modeling microtubule dynamic instability, Bulletin of Mathematical Biology, 81 p. 722–758 (2019)
[4] B. Perthame. Transport equations in biology, Springer.

Slides [talk]