smai.emath.fr/maddmaths/7/

Accès au numéro 6

Newsletter #7 - Mars 2015

Version Smartphone | Version en ligne | Nous contacter | S'abonner | Se désabonner | Suggérer à un(e) ami(e)

MaddMaths
Edito

Un ZOOM sur les métiers des maths et de l'informatique est sorti le jour de π-day (3/14/15) et du lancement de la semaine des mathématiques. En cette période de choix d'orientation pour les futurs bachelier-e-s, cette belle brochure, réalisée par l'ONISEP en partenariat avec les sociétés savantes, peut être téléchargée gratuitement. N'hésitez pas à lire ces témoignages qui illustrent la diversité des débouchés passionnants qu'offrent les formations de maths & info et, surtout, relayez l'information autour de vous !

En espérant que ce 7ème numéro de MADD Maths vous plaise, nous vous souhaitons une très bonne lecture et rendez-vous dans quelques mois pour le prochain numéro.



L'équipe de rédaction de la lettre MADD Maths.



Améliorer ses performances de course à pied...grâce à des équations mathématiques !

running Quelle est la première chose qui vous vient à l'esprit quand vous pensez au sport et aux mathématiques ? Très probablement, la craie et le fromage, non ?


Croyez-le ou non, une recherche récente, menée par les mathématiciens français Amandine Aftalion (Laboratoire de Mathématiques de Versailles) et Frédéric Bonnans (École Polytechnique), a montré comment le sport pouvait grandement bénéficier des apports des mathématiques.


Lorsqu'on l'interroge sur la motivation derrière cette étude, Amandine Aftalion dit que son amour pour les mathématiques et le sport (elle pratique régulièrement la natation) l'a convaincue qu'on pouvait utiliser des équations mathématiques pour améliorer la physiologie humaine et atteindre une performance athlétique optimale !


Atteindre une performance athlétique optimale !

Afin de mener à bien leur étude, les mathématiciens ont choisi un sport relativement simple, la course à pied. Ils modélisent mathématiquement une course à l'aide d'équations différentielles, les résolvent et ainsi prédisent une stratégie optimale pour courir une distance donnée en un minimum de temps. Leur modèle prend en compte des paramètres physiologiques du coureur, tels que la consommation maximale d'oxygène et l'énergie totale anaérobie disponible, et implique plusieurs équations différentielles couplant les variables externes au coureur : la vitesse, la force de propulsion, les forces de frottement, et l'énergie anaérobie que le corps utilise en cas de déficit d'oxygène.


Ce modèle est construit sur un ancien modèle développé par le célèbre mathématicien Joseph Keller il y a près de quarante ans. Keller, coureur passionné lui-même, a d'ailleurs reçu le prix Ig Nobel en 2010, pour sa contribution mathématique sur la question de savoir pourquoi la queue de cheval d'un coureur balance de droite à gauche alors que sa tête va de haut en bas !


Le modèle de Keller faisait l'hypothèse que lors d'une course, un athlète devait maintenir sa vitesse constante pour atteindre des performances optimales. Le modèle d'A. Aftalion et F. Bonnans, lui, suppose la vitesse variable. C'est un fait bien connu des sportifs : faire varier sa vitesse permet de mieux dépenser son énergie et de courir plus longtemps.


Maintenant, comment les scientifiques résolvent-ils un système non-linéaire d'équations différentielles ? Évidemment, comme les équations font intervenir plusieurs paramètres et sont couplées, ce n'est pas exactement le type d'équation que vous avez appris à l'école. Mais l'utilisation d'un « solveur » de contrôle optimal développé par une équipe de l'INRIA (Institut français de recherche en informatique et automatique) a permis d'obtenir une solution numérique complète. En particulier, cela donne accès à la vitesse et à la dépense énergétique à chaque instant de la course.


De plus, il est maintenant possible d'identifier les paramètres physiologiques grâce à des mesures prises à distances régulières dans la course, dès qu'on a une bonne estimation de la consommation maximale d'oxygène. Cela est suffisant pour faire fonctionner le programme et pour prévoir une course idéale. L'outil peut prédire comment une amélioration de l'absorption maximale d'oxygène ou d'énergie anaérobie totale peut améliorer ou modifier la vitesse, les temps intermédiaires et le nombre de calories perdues dans la course. Il peut également donner des indications pour mieux courir en montée, en descente ou contre le vent. Les prédictions correspondent étroitement aux stratégies réelles utilisées par les athlètes professionnels. Cet outil, combiné à la technologie moderne, pourra être utile aussi bien à un semi-professionnel, pour l'aider à améliorer sa performance, qu'à un coureur amateur, qui n'a pas de coach mais qui a besoin de conseils sportifs personnalisés, mais aussi à un coureur du dimanche, qui veut connaître le nombre exact de calories dépensées dans la course pour optimiser sa perte de poids.


L'étude a commencé avec des stratégies de course à pied, mais l'objectif d'Amandine Aftalion et de Frédéric Bonnans est d'adapter le modèle à d'autres sports d'endurance, comme le cyclisme, la natation, le triathlon ou le ski de fond.


Un nouveau modèle mathématique explique pourquoi les hipsters se ressemblent tous.

Jonathan Touboul, chercheur au Collège de France, a montré pourquoi les hipsters, ces anticonformistes contemporains, finissent par se ressembler un peu tous.


hipster Dans l'article intitulé « L'effet hipster : quand tous les anticonformistes finissent par se ressembler » récemment paru sur arXiv, J. Touboul explique mathématiquement pourquoi les hipsters, essayant toujours d'être différents, finissent par faire tous la même chose en même temps et à la fin se ressemblent.


Pour décrire les hipsters, Touboul fait référence à un modèle classique de la physique statistique, les verres de spin, en considérant une population d'individus en mesure de prendre des décisions. Ces décisions peuvent être prises soit en conformité ou contre la majorité de la population. Les hipsters, en agissant par pur esprit de contradiction, choisissent toujours le contraire de ce que fait la majorité.


Le modèle prend en considération le délai nécessaire à l'information pour être communiquée, c'est-à-dire le retard des hipsters à enregistrer les décisions des autres. En fait, s'ils savaient immédiatement les modes du moment ou les décisions prises par la majorité de la population, alors le modèle ne serait en mesure de représenter aucune structure particulière de cette composante « alternative » de la société. Mais dans le monde réel il est impossible de connaître les décisions des autres en temps réel, cela prend forcément un peu de temps.


Pour décrire les hipsters, un modèle classique de la physique statistique

C'est précisément à cause de ce retard que les alternatifs peuvent se synchroniser par inadvertance avec les autres. En considérant le retard et le choix fait par le propre réseau des connaissances, les décisions initiales des hipsters vont se synchroniser, car tous sont enclins à choisir la même chose.


Le modèle montre comment, contrairement aux systèmes coopératifs, une population d'individus prenant des décisions à l'encontre de la majorité subit des transitions de phase. Lorsque les hipsters sont trop lents pour détecter les tendances, ils continuent à faire les mêmes choix et restent donc en corrélation, tandis que leur tendance évolue dans le temps comme une fonction périodique. Cela est vrai lorsque la majorité de la population est constituée d'hipsters. Sinon, les hipsters seront, encore une fois, en grande partie alignés, vers une direction constante en opposition aux choix traditionnels.


L'auteur de l'étude explique enfin que l'intérêt de sa recherche dépasse la question des hipsters. En effet, cette étude peut avoir des implications importantes dans la compréhension de la dynamique des réseaux des circuits d'inhibition du cerveau, les stratégies d'investissement en finance ou la compréhension des dynamiques émergentes dans les sciences sociales ; domaines dans lesquels des retards de communication et la géométrie des systèmes semblent être décisif.


Alphabet : G comme Gradient

Tout phénomène naturel a lieu à cause de la présence d'un gradient. Un gradient topographique (avec de la pluie) génère une rivière et un gradient d'énergie élastique, accumulée petit à petit à l'intérieur de la croûte terrestre, est responsable d'un tremblement de terre. Quand nous faisons les courses au rayon de fruits et légumes du supermarché, nous gelons : c'est la faute du gradient de température. Quand nous en sortons, nous avons l'impression de crever de chaud. Encore la faute au gradient, seul responsable de cette variation thermique.


gradientIl y a plusieurs façons de mesurer le changement des choses et, concernant le gradient, la question est relative. Le choc thermique que nous subissons en faisant les courses est dû au fait que hors du supermarché il y a trente degrés à l'ombre et, passé la porte, la température passe rapidement a quinze degrés. Un saut de quinze degrés en quelques mètres. Changement, oui, mais rapide. Ou encore plus précisément, changement raide. Ce que nous mesurons, ce n'est pas la différence absolue entre deux valeurs, mais la différence relativement à la longueur de la distance parcourue en cette transition. Il s'agit d'un rapport entre dimensions : saut de température divisé par la distance parcourue.


Qui y voit une similitude avec le concept de dérivée est sur la bonne route : le gradient est, pratiquement, une dérivée. Mais avec une différence : tandis que la dérivée détermine la pente d'une courbe et nous restreint à un parcours unidimensionnel, le gradient a la liberté d'un déplacement bien plus grand.


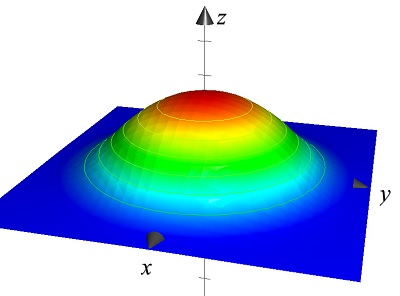
Revenons à l'exemple de la température. Imaginons une pièce et, pour simplifier, arrêtons l'avancement du temps. À chaque point de la pièce on peut y associer sa valeur de température. Près des chauffages (allumés si on est en hiver) la température est élevée, près des fenêtres (ouvertes... même en hiver !) elle est basse. En considérant un point de départ dans la pièce, nous pouvons déterminer plusieurs directions de déplacement (en haut, en bas, à droite, à gauche, en diagonale, transversalement, ...) et pour chacune d'entre elles il est possible de déterminer le rapport correspondant entre la variation de température et la distance parcourue. Ainsi et en passant à la limite dans les longueurs des distances au dénominateur, à chaque point de la pièce est associé un objet mystérieux qui codifie la rapidité des changements thermiques selon la direction de déplacement.


En mathématiques l'objet mystérieux a un nom précis, il s'appelle "différentielle", et il vit dans le monde de l'Algèbre Linéaire. Pour un miracle du monde qui nous entoure, il est possible de décrire cette fantomatique différentielle par une quantité plus facile à manipuler : le gradient. Dans l'exemple précédent, en chaque point (de la pièce), le gradient (de température) est identifié à un vecteur dont la direction correspond à celle de variation maximale, et la longueur décrit la rapidité de variation (de température). Notre pièce est ainsi peuplée de vecteurs qui, point par point, indiquent selon quelle direction nous devons nous déplacer si nous cherchons un endroit plus chaud.


nabla Une fois l'objet défini – dont le symbole est un triangle isocèle à tête en bas, appelé "nabla" à cause d'une ressemblance avec un type d'harpe de la Grèce antique - et le concept formalisé, l'amusement est garanti. Laissant à nouveau le temps s'écouler, et faisant confiance à Jean-Baptiste Fourier, nous pouvons supposer que la chaleur se déplace dans la pièce selon la direction opposée à celle indiquée par le gradient, donc dans la direction de variation maximale de température et du chaud vers le froid. Utilisant papier et stylo pour compléter le bilan de quantités en jeu, nous retrouvons la célèbre "équation de la chaleur" qui décrit l'évolution des conditions thermiques de la pièce à partir de maintenant jusqu'à la fin des jours.


De la même façon, de nombreux autres modèles existent dans lesquels les variations temporelles d'une quantité observée sont guidées par un gradient. Avec un seul mot et un seul instrument nous pouvons jouer des musiques apparemment différentes : le déplacement de charges électriques (loi d'Ohm), l'hydraulique et la construction des fontaines de Dijon (loi de Darcy), le transport de masse (loi de Fick), etc. Les contextes, les problèmes et les significations physiques changent, mais au bout du compte il s'agit toujours de la mélodie du gradient.


Traduit à partir de la version originale en italien de Corrado Mascia avec l'autorisation de l'auteur.


Vie de Mathématicien(ne) : Julie Antic

verneuil Que font les mathématiciens ? Julie Antic s'exprime sur le sujet à travers une interview que nous lui avons proposée.

  • D'où vient votre passion pour les mathématiques ? Et pourquoi avez-vous décidé d'étudier les mathématiques ?

    Depuis l'école primaire, j'ai toujours préféré les mathématiques aux autres matières. Elles m'ont toujours semblé plus simples par leur caractère manichéen, si rassurant : c'est juste ou c'est faux, pas de nuances subjectives, difficiles à appréhender... Ma réelle passion pour les mathématiques s'est construite au fur et à mesure, mais principalement à partir du lycée, quand on commence à découvrir toute l'étendue des connaissances mathématiques, et à deviner leur pouvoir.

  • Est-ce que vous pouvez nous parler de votre parcours scolaire/universitaire ?

    J'ai passé un bac scientifique avec la spécialité mathématiques en 2001. Ensuite, je suis entrée dans une école d'ingénieur avec prépa intégrée : l'INSA (Institut National des Sciences Appliquées) à Toulouse. J'étais rassurée par ce cursus moins périlleux que les prépas classiques. De plus, il me permettait de repousser à plus tard le choix entre une carrière dans les mathématiques (c'était ma matière préférée, mais j'avais du mal à imaginer les métiers possibles) et la biologie (je n'étais pas fan de la chimie mais j'étais très attirée par les métiers autour de l'agriculture, de l'agronomie, de l'environnement). À l'issue des deux années de prépa, j'étais fermement décidée à poursuivre dans les mathématiques. J'ai donc choisi la filière mathématiques et modélisation, puis la spécialité statistiques.

  • Avez-vous eu envie de poursuivre vos études universitaires par une thèse ? Est-ce que vous vouliez continuer votre carrière dans l'université ?

    Après avoir obtenu mon diplôme d'ingénieur, j'ai poursuivi mes études par une thèse CIFRE (conventions industrielles de formation par la recherche). Pour être honnête, cette thèse était avant tout motivée par une envie de profiter un peu plus longtemps de la vie d'étudiante... A priori, j'étais plus attirée par l'industrie que par une carrière universitaire. Mais cette thèse était le moyen idéal pour se décider puisqu'elle m'a fait découvrir la recherche universitaire, l'enseignement et l'industrie. Finalement, j'ai beaucoup apprécié l'enseignement et l'industrie, et j'ai réalisé que la recherche me convenait moins bien : elle offre plus de liberté et d'autonomie, mais elle favorise moins le travail en équipe et n'apporte pas la stimulation créée par des objectifs et des échéances fermes.

  • Comment êtes-vous entrée dans le monde industriel ?

    Je suis entrée dans le monde industriel très progressivement via la thèse CIFRE. Elle m'a permis de travailler pendant trois ans en partenariat avec l'industrie pharmaceutique, et de passer 6 mois au sein de leur équipe dans leurs bureaux. Après ma thèse, j'avais envie de travailler dans l'industrie. Le plus naturel aurait été de poursuivre dans l'industrie pharmaceutique, mais je n'ai pas réussi à trouver de poste à Toulouse (ville à laquelle je suis très attachée). J'ai donc élargi mes recherches et finalement été recrutée dans l'industrie spatiale. Mon supérieur était intéressé par mes compétences en mathématiques et mon goût pour l'industrie et les applications, même si je ne connaissais rien au spatial ! La polyvalence des mathématiques est une grande force.

  • Pourquoi avez-vous choisi cette carrière ?

    Je n'ai pas vraiment choisi ma carrière car j'avais beaucoup de mal à imaginer la carrière d'un mathématicien dans l'industrie. Je me suis laissée porter par mes goûts et les opportunités proposées au fur et à mesure de mes études. Cependant, j'ai toujours veillé à ce qu'il y ait de réels débouchés professionnels à la sortie. Concernant les mathématiques, j'ai été vite rassurée : les industries aérospatiales (pour le calcul numérique) et la finance (pour les statistiques) sont aujourd'hui de très gros recruteurs de mathématiciens. J'ai découvert ensuite qu'il existe aussi des opportunités dans beaucoup d'autres filières.

  • Que faites-vous actuellement (plus en détail) ?

    Je développe des logiciels qui aident à la conception des antennes satellites. Les antennes satellites sont souvent méconnues, mais elles sont omniprésentes dans notre vie de tous les jours. Elles permettent :
    de recevoir la télévision grâce à une parabole
    de se localiser n'importe où sur Terre (avec le système GPS et très bientôt Galiléo)
    de prendre des « photos » de la Terre (pour google maps par exemple) ou de l'espace,
    de faire des mesures très utiles pour la météo et l'étude de notre environnement (hauteur des vagues, surface de forêts, de banquises...)etc.
    Plus précisément, mon travail consiste à implémenter dans des logiciels une modélisation des antennes la plus proche possible de la réalité. Ces logiciels sont ensuite utilisés pour optimiser la conception des antennes, prédire leurs performances… Plus les modèles mathématiques arrivent à reproduire de manière fiable la réalité, plus ils permettront d'économiser la fabrication de prototypes, la réalisation de campagnes de mesures très coûteuses, et de trouver rapidement l'antenne la plus adaptée au besoin du client. L'enjeu est donc de proposer des modèles de plus en plus complexes, mais avec des temps de calcul raisonnables !

  • Est-ce que vous êtes satisfaite de votre choix ?

    Je suis très satisfaite de mon choix de carrière. Mon poste d'ingénieur me permet de faire des mathématiques et de voir très concrètement à quoi elles servent : la mise en service d'un satellite est un aboutissement très concret ! En plus de ce travail d'ingénieur, j'ai la chance d'enseigner quelques heures par an à des élèves ingénieurs. Cette tâche de transmission est pour moi très gratifiante.

  • Quelle est l'importance des mathématiques dans votre métier ?

    Les mathématiques jouent un rôle très important pour trouver/améliorer une modélisation, ou proposer de nouveaux algorithmes (pour réduire les temps de calcul ou améliorer leur convergence). Je les utilise aussi souvent pour des calculs « simples » très divers : géométrie, dérivation, intégration… Malheureusement, je n'ai pas la chance de faire des mathématiques tous les jours ! Le quotidien comporte aussi une part d'informatique et d'administratif.

  • Pouvez-vous décrire un projet dans lequel les mathématiques ont joué un rôle important ?

    C'est ma thèse qui a le plus fait appel aux mathématiques. Elle était appliquée à la pharmacocinétique : l'étude de l'élimination des médicaments par notre organisme (sous quelle forme, à quelle vitesse…). La pharmacocinétique est essentielle pour trouver le meilleur dosage (c'est-à-dire celui qui permettra de maximiser les effets du médicament tout en limitant ses effets secondaires). Les variables pharmacocinétiques sont généralement similaires chez tous les individus. Les principaux modèles mathématiques supposent donc que ces variables suivent une distribution « normale », c'est-à-dire que les valeurs les plus proches de la moyenne sont les plus probables. Cependant pour certaines molécules, on observe des différences dans la population des patients, qui sont difficiles à expliquer. Dans ce cas, l'hypothèse de normalité des variables n'est pas valable. Ma thèse visait donc à proposer des méthodes de modélisation qui ne reposent pas sur cette hypothèse. Elle a nécessité beaucoup d'études bibliographiques, l'implémentation de nombreux algorithmes, et des recherches principalement en optimisation.

  • Est-ce que vous êtes satisfaite de « l'application » de votre connaissance des mathématiques ?

    Les applications sont le moteur principal de ma motivation. Je trouve très stimulant de travailler dans des équipes pluridisciplinaires, pour plusieurs raisons. Premièrement, je retrouve les caractéristiques de l'enseignement : plaisir de l'échange, nécessité de synthèse et de pédagogie, extraction des caractéristiques essentielles des modèles (domaine d'application, hypothèses principales) sans se perdre dans les détails complexes des algorithmes. De plus, j'apprends énormément car il est indispensable de très bien comprendre l'application visée pour proposer un modèle pertinent. Ces échanges avec des personnes, généralement passionnées, sont extrêmement enrichissants.

  • Changeriez-vous quelque chose dans votre vie comme mathématicienne ? Quels sont vos projets pour l'avenir ?

    Mon travail est globalement très intéressant, cependant il comporte une part de tâches répétitives ou peu intéressantes. Par exemple, je dois parfois implémenter des logiciels, certes utiles, mais très peu exigeants intellectuellement. Dans l'idéal, j'aimerais toujours avoir l'occasion d'apprendre et de progresser. Pour l'avenir, j'ai l'impression que je vais devoir choisir entre une spécialisation en mathématiques/modélisation (quitte à élargir le domaine d'application) ou dans les antennes satellites (en mettant un peu de côté les mathématiques). Je n'ai pas encore pris de décision. Comme à mon habitude, je pense qu'elle dépendra essentiellement des opportunités qui se présenteront. Dans tous les cas, j'apprécie beaucoup la grande diversité des possibilités offertes quand on a un profil « maths appli ».

  • Selon vous, quelles sont les raisons qui font des mathématiques le sujet le plus difficile et pas toujours aimé parmi les autres sujets scolaires ?

    Pour moi, le problème est que les mathématiques sont aujourd'hui plus utilisées comme moyen de sélection des élèves que pour leur utilité dans la vie courante et professionnelle. Il me semble que cela met beaucoup de pression sur cette matière, et potentiellement de dégoût. Les programmes scolaires en mathématiques me semblent plutôt exigeants (par rapport aux autres pays) et peu orientés vers les applications concrètes. Ne devrait-on pas apprendre très tôt comment calculer les intérêts d'un prêt ? À interpréter des données statistiques, largement utilisées comme arguments par les médias, les politiques ?

  • Que conseilleriez-vous aux mathématiciens qui veulent entrer dans le domaine industriel ?

    Je les encouragerais ! Les mathématiques offrent des carrières intéressantes. Aujourd'hui, il n'existe pas de métier-type du « mathématicien dans l'industrie ». C'est un peu déroutant car on n'entre pas dans un cadre de poste bien connu et identifié (j'ai souvent du mal à expliquer que je ne suis ni informaticienne, ni ingénieur antenne). Mais cela offre une grande liberté. On peut adapter notre poste à nos aptitudes et à nos goûts : plus orienté vers les mathématiques, l'informatique, les applications...


Le questionnaire de Proust : Virginie Bonnaillie-Noël

bonnaillie Virginie Bonnaillie-Noël est Directrice de recherche au CNRS au département de mathématiques et applications de l'Ecole normale supérieure depuis 2014. Elle a été faite Chevalier de l'Ordre National du Mérite en 2011 et a reçu le prix Irène Joliot-Curie en 2009. Elle a reçu également la médaille de bronze du CNRS en 2008. Ses travaux de recherche portent notamment sur les supraconducteurs, l'équation de Schrödinger, les équations de Navier en utilisant l'analyse asymptotique, l'optimisation ou les simulations numériques.

  • Ma vertu préférée en mathématiques

    La diversité.

  • Le principal trait de mon caractère mathématique

    L'engagement.

  • La qualité que je préfère chez les mathématiciens

    L'honnêteté.

  • La qualité que je préfère en mathématiques

    La nouveauté.

  • Mon principal défaut comme mathématicienne

    La dispersion.

  • Ma lecture mathématique préférée

    Braes, Rudin, Reed-Simon, Fournais-Helffer.

  • Mon rêve comme mathématicienne / Mon cauchemar comme mathématicienne.

    Avoir du temps / Ne pas réussir à tenir les délais

  • La faiblesse principale des mathématiques

    La difficulté parfois de les communiquer à l'extérieur

  • La mathématicienne que je voudrais être

    Aucune en particulier

  • Le théorème que je préfère

    Les théorèmes de convergence (théorique ou d'analyse numérique).

  • L'application des mathématiques que je préfère

    L'application à la médecine.

  • Les mathématiciens qui m'ont orientée

    François Alouges, Bernard Helffer, Maria Esteban, Michel Pierre, Laurent Di Menza, Thierry Gallay, Patrick Gérard, Jean Voedts... et bien d'autres chaque jour !

  • Les mathématiciens qui m'ont dissuadée

    Disons que certains enseignants m'ont « convaincue » de ne pas m'orienter vers certains domaines des mathématiques...

  • Le nom de variable que je préfère

    x, l'inconnu(e).

  • Le type de calcul que je préfère

    Les simulations numériques et les développements asymptotiques.

  • Le type de calcul que j'utilise

    Les simulations numériques et les développements asymptotiques.

  • Le type de calcul que je trouve le plus ennuyeux

    Certains calculs explicites : on repousse souvent le moment où on devra s'y confronter.

  • Les dénominations mathématiques que je préfère (théorème, corollaire...)

    Exemple

  • L'entreprise scientifique que j'estime le plus

    L'ordinateur

  • Le don de la nature que je voudrais avoir.

    La faculté d'avoir besoin de très peu dormir (voire pas du tout...)

  • Comment j'aimerais qu'on se souvienne de moi comme mathématicienne

    Comme d'une mathématicienne épanouie et pleinement investie dans son travail à la fois de recherche, d'animation et de diffusion.

  • L'état présent de mes recherches

    Arrivée dans un nouveau laboratoire très récemment, je voudrais lancer de nouvelles collaborations et terminer tout ce qui est déjà en chantier...

  • La faute qui m'inspire le plus d'indulgence

    Une erreur de calcul.

  • Ma devise

    Ce n'est qu'en essayant continuellement que l'on finit par réussir...En d'autres termes, plus ça rate et plus on a de chances que ça marche...

  • Pourquoi la recherche mathématique est-elle masculine ?

    Ce n'est pas la recherche qui est masculine mais la majorité des gens qui la font. Pour le moment... Beaucoup d'actions sont mises en place pour arriver à davantage de mixité.

  • Dans quelle mesure le travail compte-t-il dans la résolution de problèmes mathématiques ?

    Sans travail, il n'y a pas de résultat !

  • Dans quelle mesure le formalisme compte-t-il ?

    Énormément : bien formaliser le problème constitue le point clé du problème et donne une bonne partie de sa résolution.

  • Mathématiques et grammaire sont-elles liées ?

    Pour ma part, pas trop. Mais je peux comprendre que ça le soit pour certaines personnes.

  • Parlez-vous "mathématique" correctement ?

    Je l'espère... mais malheureusement avec quelques fautes de temps en temps... que j'essaie de corriger.

  • À quel point faut-il être douée pour réussir en mathématique ? Pourquoi faut-il avoir moins de trente ans ?

    Je ne pense pas qu'il faille être doué outre mesure pour réussir. Je pense surtout qu'il faut être motivé et ne pas hésiter à s'acharner parfois sur quelques problèmes. Quant à avoir moins de trente ans, je ne sais pas. J'ai largement dépassé les 30 ans et j'espère que je pourrai encore avoir quelques réussites mathématiques !

  • Êtes-vous douée ? Depuis quand ?

    Non, je ne suis pas spécialement douée. Je suis plutôt travailleuse et j'essaie d'être aussi organisée que possible.



Version Smartphone | Version en ligne | Nous contacter | S'abonner | Se désabonner | Suggérer à un(e) ami(e)