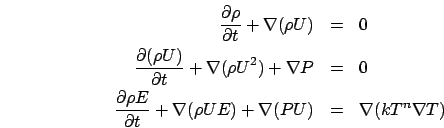Propagation des incertitudes en dynamique des fluides compressibles.
Sujet proposé par le CEA/Bruyères (R.Sentis).
En dynamique des fluides, on sait que la propagation des chocs dépend
des caractérististiques du fluide par l'intermédaire de l'équation d'état reliant la pression à l'énergie interne.
L'objectif de ce travail est d'évaluer la sensibilité de la solution
par rapport aux différents paramètres intervenant dans l'équation d'état ou dans le coefficient de conductivité thermique.
Plus précisémment, on considère le système Euler
compressible avec conduction thermique, où 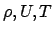 désignent la
densité, la vitesse et la température du fluide, l'énergie
interne est donnée par
désignent la
densité, la vitesse et la température du fluide, l'énergie
interne est donnée par 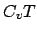 et l'énergie totale par
et l'énergie totale par
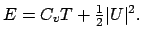 En géométrie 1D, il s'écrit
En géométrie 1D, il s'écrit
On suppose que l'on a juxtaposition de 2 fluides (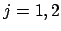 ), chacun étant
caractérisé par une équation d'état de référence
), chacun étant
caractérisé par une équation d'état de référence
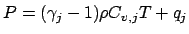 et une coefficient
et une coefficient 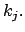 Les 8 paramètres
Les 8 paramètres
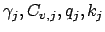 sont des données
sont des données
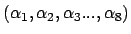 entachées d'une certaine
incertitude
entachées d'une certaine
incertitude
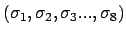 . En
supposant que les variations de ces 8 paramètres sont petites, on veut déterminer l'incertitude sur la solution du système au bout d'un
temps fixé. Si on suppose que la variation
. En
supposant que les variations de ces 8 paramètres sont petites, on veut déterminer l'incertitude sur la solution du système au bout d'un
temps fixé. Si on suppose que la variation
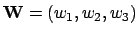 de
de
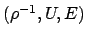 sont petites, on est alors
conduit au système linéarisé qui s'écrit
sont petites, on est alors
conduit au système linéarisé qui s'écrit
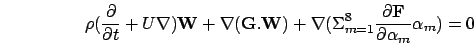 |
(1) |
Les fonctions 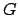 et
et 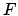 dépendent bien sûr de la solution de référence
dépendent bien sûr de la solution de référence 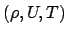 et peuvent être discontinues. Il conviendra de vérifier que ce système est du même type que celui rencontré
dans la littérature où on le traite avec des méthodes
Lagrangiennes. Puis en s'aidant éventuellement d'un code déjà
existant pour l'écoulement de base, il conviendra de résoudre numériquement le système (1) pour évaluer les incertitudes
sur la solution.
et peuvent être discontinues. Il conviendra de vérifier que ce système est du même type que celui rencontré
dans la littérature où on le traite avec des méthodes
Lagrangiennes. Puis en s'aidant éventuellement d'un code déjà
existant pour l'écoulement de base, il conviendra de résoudre numériquement le système (1) pour évaluer les incertitudes
sur la solution.