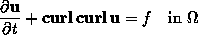
The sliding mesh-mortar method for 2D and 3D Maxwell equations
F. BEN BELGACEM A. BUFFA, Y. MADAY, F. RAPETTI
We have been working in the context of finite element approximation domain decomposition techniques for linear second order PDEs.
The aim of the project is to propose a sliding-mesh method of the simulation of electric motors. We want to calculate the induced currents in a physical system characterized by a rotating part, say rotor, and a fixed one, say stator. The law of behaviour is the system of reduced Maxwell equations when displacement currents are neglected. We use two different grids for the rotor and stator part and the rotor one spins with the physical system. The coupling is done by means of Mortar method techniques. In the 2D case the system of Maxwell equations can be reduced to a heat equation and the sliding-mesh method had been already proposed in the case of curved triangulations for both domains. We studied the generalization to the case of isoparametric finite elements since this kind of discretization is much easier to implement. Some numerical tests are available.
In the 3D case, the equation we deal with is of the type:
where
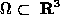 is a bounded Lipschitz domain and
is a bounded Lipschitz domain and
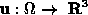 is the magnetic vector potential.
is the magnetic vector potential.
For the approximation of this kind of equation we propose the use of 3D finite elements of Nedelec type and we are studying a good definition of the Mortar method in this context. Some first error estimations have been found and some basic tools for a 3D code have been developed.