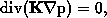
CEMRACS summer school 1998

PRESSURE DIFFUSION EQUATION & MULTIHOMOGENIZATION

Albert COHEN, Daniel GOUJOT & Roland MASSON

This subject was formulated thanks to the Institut Français du Pétrole. Mineral oil sheets fill spongy materials in the ground. Simulation is needed to improve the extraction. The pressure, given by

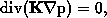
has to be computed in huge-sized materials.

Due to the cost of digging, there is little information about  K : to make a simulation, 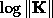is chosen to be a spatial correlated wide Gaussian tensor 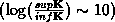, whose parameters are set by geophysicists. The background is convenient for homogenization.

Let us consider the Galerkin mass matrix in wavelet coordinates : in the square representing the operator part between subspaces W^j and W^k, there is an off-"diagonal" geometrical coefficient decay of power

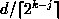where d is the number of coefficients needed to cross the off-diagonal gap.

With 1D coarse-corrected Schauder wavelets, a sufficient condition is :

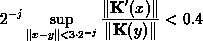
(then the decay rate is about 0.4).

ASSUMPTION : Let H^q be the graduated set of rectangular matrix with an off-diagonal decay rate of tanh(q). Let be two matrix respectively belonging to H^alpha and to H^beta : their product is assumed to be in H^alpha+beta. This generalizes the Schur lemma (saying H^q elements are invertible).

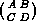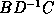Let us denote the Galerkin mass matrix in wavelet cordinates by . It follows that the Schur correction has the shape of A up to a worse decay rate : it is possible to homogenize 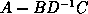one more time, dividing again the size of the matrix.

We know that the Schur reduction process keeps the condition number. Here, the multi-homogenized system should be far more well-conditionned, as homogenizing looks like smoothing .
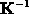