

Up: 4 A new formulation of shape optimization problem in
order to use a quasi-newton algorithm
4.1 Introduction
Optimal shape design is a branch of optimal control theory where the
control is the shape of the domain of definition of the partial differential
equation which describes the state of the system.This branch has been studied extensively in the seventies (see
[3]). The minimum
drag problem in fluid mechanics is such a problem with important industrial
applications.
There are two main ways to described a shape:
- If we know the CAD description of the shape, only a few number of
data characterize the shape, but we have to differentiate the CAD.
- In the other case, a discrete description of the shape is given. It's
easier to differentiate but the problem can be very large.
An other way is to defined each shape as a reference shape plus a linear
combination of admissible displacements:
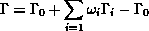
where n is small, Gammai are some admissible shapes and Gamma0 is the
reference shape which is also admissible. It is an easier way because the
admissible shapes can be defined by a CAD or a discrete description and the derivative is
computed with the respect of the coefficients omegai.
Christophe Prud'homme